- Сообщения
- 75
- Реакции
- 20
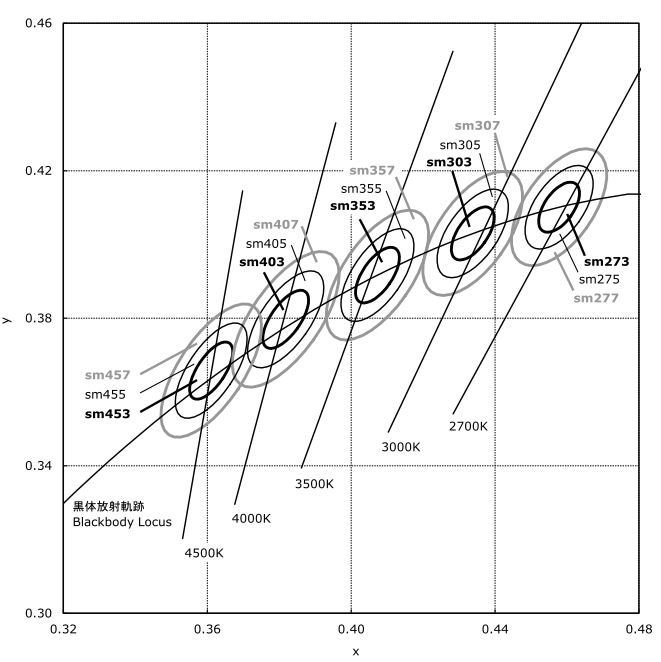
Есть координата центральной точки в CIE1931x0, y0 (вблизи АЧТ, если это важно).
Как написать формулу эллипса МакАдама вокруг этой точки в MS Exsel?
Сейчас я строю колонку значений углов phi[0, 2*пи()], по ним строю значения x=x0+a*sin(phi), y=y0+b*cos(phi+dphi). И меняя a, b, dphi кручу и плющу как хочу этот эллипс.
Как сделать чтобы это был именно эллипс МакАдама с нужным числом шагов, правильно наклоненный?
Заранее спасибо.
UPD: благодаря совету зазиповать прикрепил через файлообменник xls: 20161103 macadam ellipse
Как написать формулу эллипса МакАдама вокруг этой точки в MS Exsel?
Сейчас я строю колонку значений углов phi[0, 2*пи()], по ним строю значения x=x0+a*sin(phi), y=y0+b*cos(phi+dphi). И меняя a, b, dphi кручу и плющу как хочу этот эллипс.
Как сделать чтобы это был именно эллипс МакАдама с нужным числом шагов, правильно наклоненный?
Заранее спасибо.
UPD: благодаря совету зазиповать прикрепил через файлообменник xls: 20161103 macadam ellipse
Последнее редактирование:

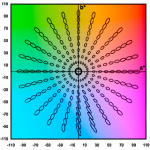
 Речь-то о светотехнике, так что испытуемые будут считать шаги скорее не цвета а света
Речь-то о светотехнике, так что испытуемые будут считать шаги скорее не цвета а света