Ответ: Простая задача
Аналитически эту задачку тоже можно решить...
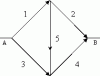
Пронумеруем ребра моста в рисунке, приведенном
Vadim_PDF так: верхние ребра моста -- 1 и 2, нижние -- 3 и 4, перемычка моста -- 5 (см. приаттаченный рисунок).
Пусть I — ток проходящий через всю конструкцию. I
k — ток, проходящий через ребро k,
Тогда I=I
1+I
3, I
1=I
2+I
5, I
3+I
5 = I
4, I
2+I
4=I (по первому правилу Кирхгофа)
Введём параметр a: I
1 = a*I, тогда I
3 = (1-a)*I
Обозначим U
k — разность потенциалов на ребре k
Тогда U
1 = I
1*R
1 = a*I*R
1,
U
3 = I
3*R
3 = (1-a)*I*R
3
U
5 = U
3–U
1 (второе правило Кирхгофа).
Отсюда I
5*R
5 = I

(1–a)*R
3–a*R
1)=I

R
3–a

R
1+R
3))
I
5 = I

R
3–a

R
1+R
3))/R
5
Аналогично, введем параметр b: I
2 = b*I, тогда I
4 = (1-b)*I
Тогда U
2 = b*I*R
2, U
4 = (1-b)*I*R
4
U
5 = U
2 –U
4, отсюда I
5 = I

–R
4+b

R
2+R
4))/R
5
Итак, имеем:
I
5 = I

R
3–a

R
1+R
3))/R
5,
I
5 = I

–R
4+b

R
2+R
4))/R
5
Но ещё мы знаем, что I
5 = I
1 – I
3, т.е. I
5 = (a–b)*I
Получаем: (а–b)*R
5 = R
3–a

R
1+R
3) = –R
4+b

R
2+R
4)
Получается система уравнений:
a

R
5+R
1+R
3) – b*R
5 = R
3
a*R
5 – b

R
5+R
2+R
4) = –R
4
Решаем её, и находим:
a = (R
3
R
5+R
2+R
4) + R
4*R
5) / ((R
5+R
4+R
2)

R
1+R
5+R
3) – R
5^
2)
b = (R
3*R
5 + R
4
R
1+R
5+R
3)) / ((R
5+R
4+R
2)

R
1+R
5+R
3) – R
5^
2)
Искомое сопротивление R = U/I = (U
1+U
2)/I = (a*R
1*I + b*R
2*I)/I = a*R
1 + b*R
2
Подставляем найденные значения a и b:
R = (R
1*R
2
R
3+R
4) + R
3*R
4
R
1+R
2) + R
5
R
1+R
2)

R
3+R
4)) / ((R
5+R
4+R
2)

R
1+R
5+R
3) – R
5^
2)
Если R
1 = R
2 = R
5 = R
4 =1, R
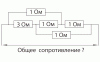
3 = 3, то R=(4+6+8)/(3*5-1) = 18/14 = 9/7 Ом
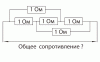
Если все сопротивления равны 1, то R=(2+2+4)/(3*3-1) = 8/8 = 1 Ом




 (1–a)*R
(1–a)*R