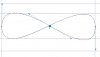
Постановка задачи такая: отрисовать векторно фигуру "Лемниската" в Illustrator.
Есть всем известная кривая - "бесконечность", она же "лемниската Бернулли".
По-простому - две капли, отталкивающиеся друг от друга хвостами.
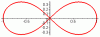
Но капля капле рознь, посему для определенности эта кривая в математике описывается конкретным уравнением.
("множество точек, произведение расстояний r1 и r2 которых до двух данных точек F1, F2 (фокусов) равно квадрату междуфокусного расстояния")
Поэтому не представляет труда отрисовать лемнискату в графиках любого математического пакета: например, MathCad, Mathematica и пр.
А вот как бы после этого получить ее векторное изображение в Illustrator?
Какие есть способы? (до трассировки, как первый способ, догадался и сам)
Есть всем известная кривая - "бесконечность", она же "лемниската Бернулли".
По-простому - две капли, отталкивающиеся друг от друга хвостами.

Но капля капле рознь, посему для определенности эта кривая в математике описывается конкретным уравнением.
("множество точек, произведение расстояний r1 и r2 которых до двух данных точек F1, F2 (фокусов) равно квадрату междуфокусного расстояния")
Поэтому не представляет труда отрисовать лемнискату в графиках любого математического пакета: например, MathCad, Mathematica и пр.
А вот как бы после этого получить ее векторное изображение в Illustrator?
Какие есть способы? (до трассировки, как первый способ, догадался и сам)