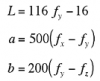Существует ли в природе какой-нибудь цветовой профиль (не матричный, наверное, и скорее всего многоканальный), который бы более-менее аппроксимировал область воспринимаемых цветов? Ну, то есть который на диаграмме цветности xy давал бы охват в виде той самой подковы. Или вот, по идее, когда Линдблум изображает «Lab gamut» — это же не ручной расчёт картинки, наверное? Или когда он же приводит величины «Lab Gamut Efficiency» и «Coding Efficiency» — откуда-то ведь он это берёт?
Профиль зрительной системы
- Автор темы Samsonov
- Дата начала
- Статус
Ответ: Профиль зрительной системы
Далее. Все эти построения касаются т.н. предметных стимулов. И сейчас я понимаю, что это правильно, потому как ежели фотометрическая яркость стимула не превышает фотометрическую яркость стимула адаптирующего (интегральная фотометрчиеская яркость сцены), то зрение не в состоянии идентифицировать природу светового потока -- отраженный он или испущенный.
Вместе с тем, Манселловский атлас претендует на то, что в нем представлены образцы всех насыщенностей, которые могут дать в природе стимулы предметные.
P.S. Голубая мечта идиота приобрести Манселловский атлас в личное пользование...
Из мансселовского атласа. Существуют LUT-ы, описывающие манселловский атлас, один из таких LUT-ов -- UPLab.Samsonov сказал(а):
Далее. Все эти построения касаются т.н. предметных стимулов. И сейчас я понимаю, что это правильно, потому как ежели фотометрическая яркость стимула не превышает фотометрическую яркость стимула адаптирующего (интегральная фотометрчиеская яркость сцены), то зрение не в состоянии идентифицировать природу светового потока -- отраженный он или испущенный.
Вместе с тем, Манселловский атлас претендует на то, что в нем представлены образцы всех насыщенностей, которые могут дать в природе стимулы предметные.
P.S. Голубая мечта идиота приобрести Манселловский атлас в личное пользование...
Ответ: Профиль зрительной системы
Хотя сам вопрос и несложен, но во избежание путаницы предлагаю начать разбираться с вопросом HVS (human visual space) с понятия локус и maximum saturation method. Как видно из примера (см. аттач), он определяется из cmf (color matching function).
Существует. Но не профиль.Samsonov сказал(а):
Хотя сам вопрос и несложен, но во избежание путаницы предлагаю начать разбираться с вопросом HVS (human visual space) с понятия локус и maximum saturation method. Как видно из примера (см. аттач), он определяется из cmf (color matching function).
Чуть уточню. Для определения границ HVS атлас не нужен, границы элементарно вычисляются по дельта-функции. Достоинство атласа в другом - uniformity (перцептуальное). Равный шаг.Alexey Shadrin сказал(а):
Ответ: Профиль зрительной системы
Саша, то, что мы получаем из трихроматических кривых Стандартного наблюдателя -- это локус максимальных цветностей, то есть локус максимальных разносов колбочковых откликов. Об ощущениях этот локус не говорит ничего.sabos сказал(а):
Ответ: Профиль зрительной системы
Область воспринимаемых стимулов -- это комплект монохроматических стимулов видимой части спектра.
Характер воздействия монохроматов на колбочковый аппарат человека графически представляет собой дугу на xy-диаграмме.
Фигура в перцепционном пространстве (L*a*b*) построена на базе манселловского атласа. Но понятно, что фигура эта ограничена характером естественных предметных стимулов, или, по крайней мере тех стимулов, которые может добавить к естественным человек при помощи искусственных красителей.
Чтобы кто-то построил перцепционную фигуру, манипулируя стимулами монохроматическими, -- мне неизвестно. Может быть кто-то сие и выполнил. Однако коль скоро прикладная ценность такого исследования сомнительна (естественные сцены почти никогда не дают монохроматов), то сомневаюсь в том, чтобы кто-то профинансировал такое исследование. Однако, я думаю (!), что данную задачу можно решить аналитически, если применить к монохроматам CIECAM02 и тем самым удовлетворить свое любопытство (но не более).
Воспринимаемых цветов не существует. Цвет -- это результат восприятия стимула. Поэтому словосочетание "воспринимаемые цвета" некорректно.Samsonov сказал(а):
Область воспринимаемых стимулов -- это комплект монохроматических стимулов видимой части спектра.
Характер воздействия монохроматов на колбочковый аппарат человека графически представляет собой дугу на xy-диаграмме.
Фигура в перцепционном пространстве (L*a*b*) построена на базе манселловского атласа. Но понятно, что фигура эта ограничена характером естественных предметных стимулов, или, по крайней мере тех стимулов, которые может добавить к естественным человек при помощи искусственных красителей.
Чтобы кто-то построил перцепционную фигуру, манипулируя стимулами монохроматическими, -- мне неизвестно. Может быть кто-то сие и выполнил. Однако коль скоро прикладная ценность такого исследования сомнительна (естественные сцены почти никогда не дают монохроматов), то сомневаюсь в том, чтобы кто-то профинансировал такое исследование. Однако, я думаю (!), что данную задачу можно решить аналитически, если применить к монохроматам CIECAM02 и тем самым удовлетворить свое любопытство (но не более).
Ответ: Профиль зрительной системы
Не по теме:
Ты, как обычно, недооцениваешь математику.
Следующим уроком (если дойдет дело) я покажу, как построить такую фигуру.Alexey Shadrin сказал(а):
Не по теме:
Ты, как обычно, недооцениваешь математику.
Ответ: Профиль зрительной системы
Вопрос в другом: нужно ли?
Саша, я имел в виду (прошу прощения за имение в виду), что мне неизвестно, чтобы кто-то построил такую фигуру на базе психофизических экспериментов. Построить ее аналитически можно (для такого построения есть необходимый минимум материала), но далеко не факт, что такое построение удовлетворительно аппроксимирует экспериментальные данные (если бы таковые проводились).sabos сказал(а):
Вопрос в другом: нужно ли?
Ответ: Профиль зрительной системы
Чем плоха Munsell renotation? LUCHI, Braun, JOSA?Alexey Shadrin сказал(а):
Аппроксимирует. Впрочем, не торопимся, придет понимание первого - дойдем и второго.Alexey Shadrin сказал(а):
Как и любая другая сверка теоретических и экспериментальных данных.Alexey Shadrin сказал(а):
Ответ: Профиль зрительной системы
Разве они строились по монохроматам, а не по предметным? Прости, я просто не встречал уточнений на сей счет: renotaion и renotaion, без пояснений.sabos сказал(а):
Ответ: Профиль зрительной системы
Чем отличается монохромат от дихромата, от широкополосного (в психофизиологическом смысле)?
Чем отличается монохромат от дихромата, от широкополосного (в психофизиологическом смысле)?
Ответ: Профиль зрительной системы
В психофизиологическом -- не знаю. В физико-физиологическом -- мерой разноса колбочковых откликов, то есть цветностью.sabos сказал(а):
Ответ: Профиль зрительной системы
Это принципиальное отличие? Оно может изменить базу (систему)?Alexey Shadrin сказал(а):
Ответ: Профиль зрительной системы
Не знаю. Просто не знаю на сколько четко мы сегодня можем спрогнозировать результат восприятия монохроматов, находящихся в реальной сцене и яркость которых не превышает адаптирующую. Но я не против аналитического расчета. Сильного отклонения он явно не даст, а коль скоро на сегодня в прикладном отношении предмет разговора -- вещь бесполезная, то, думаю, "прокатит"sabos сказал(а):
Ответ: Профиль зрительной системы
А если вспомнить про Грассмана? Или он уже "немоден"?Alexey Shadrin сказал(а):
Ценность науки теперь лишь прикладная осталась?Alexey Shadrin сказал(а):
Ответ: Профиль зрительной системы
Грассману грассманово -- он дает законы сложения стимулов. Но ув. Самсомнов, как я понял, интересуется все же ощущениями (хотя понять и непросто, что же именно его интересует?).sabos сказал(а):
Мм-м-м: опять я согрешил имением в виду -- я имел в виду, что ежели в реальных сценах практически не встречаются монохроматы, то какова научная ценность исследования искусственных ситуаций, когда в предполагаемую сцену пихают пару тройку неярких монохроматов, а потом исследуют результат их восприятия по аналитическим моделям?
Ответ: Профиль зрительной системы
.
Т.е. немоден. Я понимаю, "ощущения" - это ого! Это наше все. Здесь "примитивно организованная" математика и логика пасует, здесь нужны сакральные силы. Все, ухожу, ухожуAlexey Shadrin сказал(а):
.
Часто ли встречаются ли в реальных сценах спектры излучения ZnS:Ag+Co-on-Al2O3? Изменяет ли что либо в восприятии то, что мы аналитически можем расчитать результаты восприятия ZnS:Ag+Co-on-Al2O3? Трава на мониторе стала иначе выглядеть?Alexey Shadrin сказал(а):
Ответ: Профиль зрительной системы
Чего ты, отче? Проблема в том, что вопрос ув. Самсонова понять невозможно -- остается гадать, пока сам автор не ответит. Кстати, я, несмотря на недавно прозвучавшие призывы, в ощущения не лезу, бо считаю это преждевременным. По-моему, ты тоже...sabos сказал(а):Т.е. немоден. Я понимаю, "ощущения" - это ого! Это наше все. Здесь "примитивно организованная" математика и логика пасует, здесь нужны сакральные силы. Все, ухожу, ухожу
Принято. Убедил.
Ответ: Профиль зрительной системы
Никакой сверхточности не требуется — просто общий вид. Вот, как вы говорите, профиль UPLab построен на базе манселловских образцов — так примерно то же самое, только на базе монохромных излучателей. То есть чтобы прикинуть предельные границы, за которые точно ничего выходить не может. Понятно, что это не весь LAB-куб целиком, и в то же время даже его может не хватать (если ограничивать координаты цветности), чему Линдблум приводит наглядный пример.
Ничего сверх того не нужно. Вы почему-то всегда ищете вселенскую проблему на пустом месте.
sabos сказал(а):
Уважаемые господа! Если вы ненадолго отставите в сторонку свой снисходительный тон и ещё раз перечитаете исходный вопрос, то, надеюсь, поймёте, что речь не шла о том, как пересчитать δ(λ) в XYZ и тем более xy — соответствующие формулы широко доступны. Хотелось увидеть именно готовый цветовой профиль, который бы более-менее пристойно описывал колориметрические характеристики устройства ввода Eye-Two компании X-God.Alexey Shadrin сказал(а):
Никакой сверхточности не требуется — просто общий вид. Вот, как вы говорите, профиль UPLab построен на базе манселловских образцов — так примерно то же самое, только на базе монохромных излучателей. То есть чтобы прикинуть предельные границы, за которые точно ничего выходить не может. Понятно, что это не весь LAB-куб целиком, и в то же время даже его может не хватать (если ограничивать координаты цветности), чему Линдблум приводит наглядный пример.
Ничего сверх того не нужно. Вы почему-то всегда ищете вселенскую проблему на пустом месте.
Ответ: Профиль зрительной системы
Вложения
- Статус