- Сообщения
- 2 100
- Реакции
- 429
Очень важно уметь вычислять калибровку с нелинейных пластин в офсете — это дает возможность запихнуть шкалу в повседневную печать и привести градационную х-тику в норму. Пока здесь был представлен в основном один метод вычисления поправок к точке с нелинейных пластин — метод сложения итераций.
Я бы хотел представить/обсудить другой метод — метод Сергея Зинченко. Что-бы решить эту задачу Сергей рассматривал зависимость TV печать от TV пластина. Что-бы построить график этой зависимости надо сначала правильно определить точки этого графика на координатной плоскости. Для этого надо найти для каждой точки ее правильные координаты по оси X и по оси Y — смотрите рисунок 1 ниже.
На рисунке 1 на входе мы имеем градационную х-тику с шагом 10% — TV файл (или по простому — % в файле) — красные точки на рис. 1. Так как печать уже калибровалась перед этим — в РИПе у нас калибровка в виде или калибровочной/компенсационной кривой, или в виде поправок к точке на пластине или % на пластине или в виде TV/TVI. Неважно в каких данных у нас калибровка в РИПЕ, всегда из них можна вытянуть именно калибровочную кривую — как самое удобное представление результата калибровки в графическом виде.
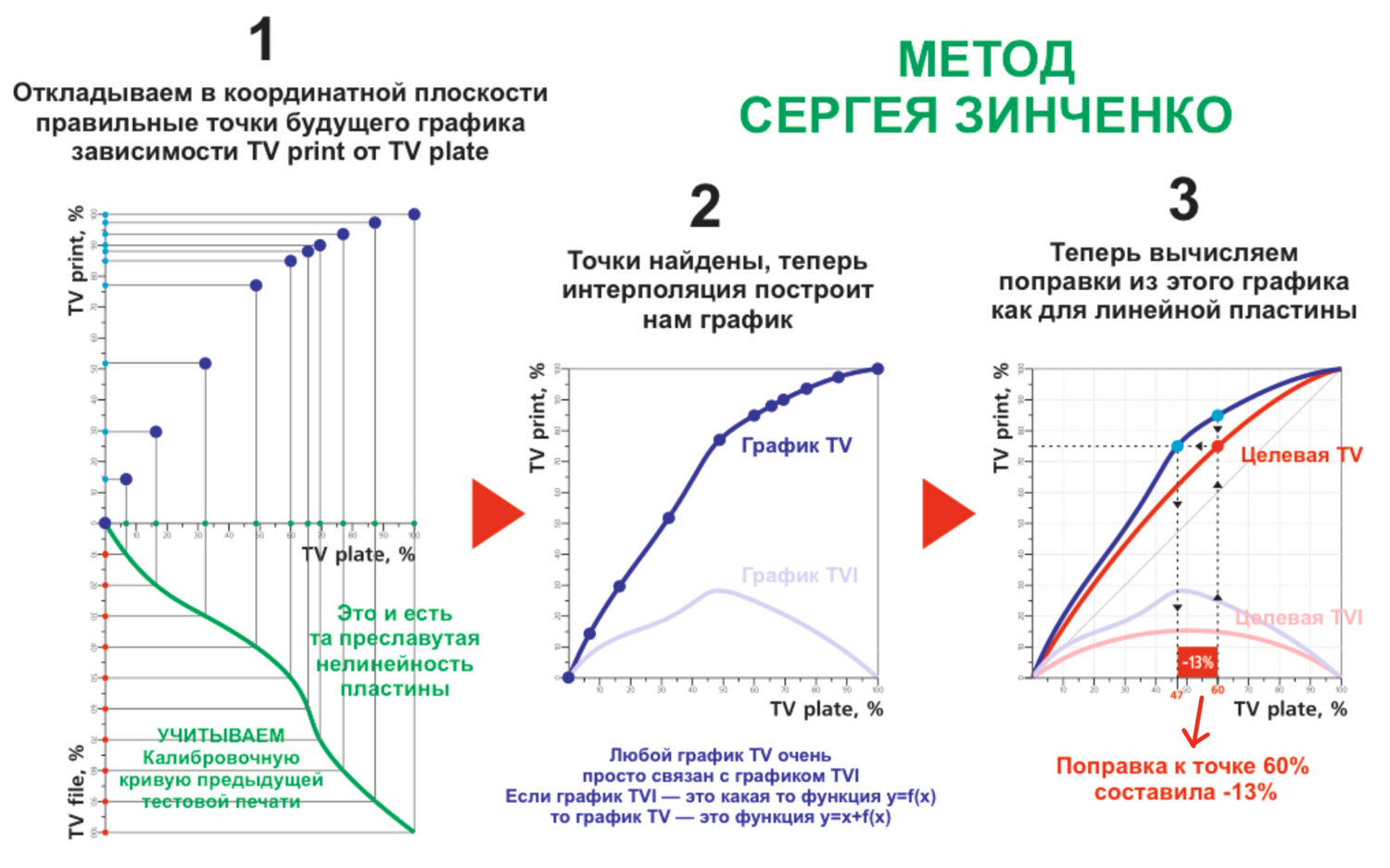
Итак, что-бы получить правильные координаты по оси X точек будущего графика, надо TV файл «пропустить» через калибровочную кривую и мы получим TV пластина (или к TV файл додать поправки к точке после первой калибровки) — это и есть учет нелинейности пластины — рис. 1 — красные точки перешли в зеленые.
Что-бы получить правильные координаты по оси Y этих точек — эти координаты и есть TV печать — мы вычисляем ее из измерений XYZ по формулах ИСО:

2) Итак точки графика опредилили. Интерполяция построит нам график — плавную кривую.
3) Итак, правильный график мы получили, нелинейность пластины учли — теперь мы можем вычислять поравки к точке как для линейной пластины — рис.3 — там представленно как именно графично вычисляется поправка относительно целевой (я раньше более подробно сбрасывал графическую интерпретацию вычисления поправок с линейных пластин и на этом углублятся не буду).
Два метода вычисления с нелинейных пластин — метод сложения и метод Сергея Зинченко рассмотрено также здесь , но почему-то без ссылки на авторство и почему-то метод Сергея назвали альтернативным методом сложений итераций. Мне в названии там целых три слова не нравится:
1) Альтернативным нелогично называть математически верный метод Сергея, а математически не верный метод сложений — традиционным. Как по мне метод сложений поправок надо отбросить как неверный метод.
2) Сложений — это слово вообще не символизирует метод Сергея — там по ссылке объяснения его метода представлено как таблица Екселя и там для вычисления поправок какие-то столбцы получаются как сложение других — складываем TV файл + поправки к точке первой калибровки что-бы получить TV пластина и складываем TVI + TV файл, что-бы получить «абсолютный TVI» или по правильному TV печати. Но эти сложения вообще не существенны — они играют роль перехода от одних велечин к другим, да и как по мне TV печати и TV пластина первичные велечины по отношению к TVI и поправки. В методе Сергея нет складывания поправок — он получает результирующие поправки и старые поправки просто выбрасываются.
3) Итераций — метод Сергея не имеет отношения к итерациям.
Я бы хотел представить/обсудить другой метод — метод Сергея Зинченко. Что-бы решить эту задачу Сергей рассматривал зависимость TV печать от TV пластина. Что-бы построить график этой зависимости надо сначала правильно определить точки этого графика на координатной плоскости. Для этого надо найти для каждой точки ее правильные координаты по оси X и по оси Y — смотрите рисунок 1 ниже.
На рисунке 1 на входе мы имеем градационную х-тику с шагом 10% — TV файл (или по простому — % в файле) — красные точки на рис. 1. Так как печать уже калибровалась перед этим — в РИПе у нас калибровка в виде или калибровочной/компенсационной кривой, или в виде поправок к точке на пластине или % на пластине или в виде TV/TVI. Неважно в каких данных у нас калибровка в РИПЕ, всегда из них можна вытянуть именно калибровочную кривую — как самое удобное представление результата калибровки в графическом виде.
Итак, что-бы получить правильные координаты по оси X точек будущего графика, надо TV файл «пропустить» через калибровочную кривую и мы получим TV пластина (или к TV файл додать поправки к точке после первой калибровки) — это и есть учет нелинейности пластины — рис. 1 — красные точки перешли в зеленые.
Что-бы получить правильные координаты по оси Y этих точек — эти координаты и есть TV печать — мы вычисляем ее из измерений XYZ по формулах ИСО:
2) Итак точки графика опредилили. Интерполяция построит нам график — плавную кривую.
3) Итак, правильный график мы получили, нелинейность пластины учли — теперь мы можем вычислять поравки к точке как для линейной пластины — рис.3 — там представленно как именно графично вычисляется поправка относительно целевой (я раньше более подробно сбрасывал графическую интерпретацию вычисления поправок с линейных пластин и на этом углублятся не буду).
Два метода вычисления с нелинейных пластин — метод сложения и метод Сергея Зинченко рассмотрено также здесь , но почему-то без ссылки на авторство и почему-то метод Сергея назвали альтернативным методом сложений итераций. Мне в названии там целых три слова не нравится:
1) Альтернативным нелогично называть математически верный метод Сергея, а математически не верный метод сложений — традиционным. Как по мне метод сложений поправок надо отбросить как неверный метод.
2) Сложений — это слово вообще не символизирует метод Сергея — там по ссылке объяснения его метода представлено как таблица Екселя и там для вычисления поправок какие-то столбцы получаются как сложение других — складываем TV файл + поправки к точке первой калибровки что-бы получить TV пластина и складываем TVI + TV файл, что-бы получить «абсолютный TVI» или по правильному TV печати. Но эти сложения вообще не существенны — они играют роль перехода от одних велечин к другим, да и как по мне TV печати и TV пластина первичные велечины по отношению к TVI и поправки. В методе Сергея нет складывания поправок — он получает результирующие поправки и старые поправки просто выбрасываются.
3) Итераций — метод Сергея не имеет отношения к итерациям.
Последнее редактирование:





 Ну неграмотный я, пора бы уже привыкнуть.
Ну неграмотный я, пора бы уже привыкнуть. ![;]= ;]= ;]=](/styles/default/xenforo/smiles.rudtp/4100_5.gif)
