Ответ: Как отрисовать фигуру "бесконечность" (повернутая 8), зная ее математическое уравнение?
Хм, возможно мы говорим про разные вещи. Я высчитывал точки принадлежащие кривой безье. Не какие-то там промежуточные, а именно точки самой кривой. Родные. Такие, какими оперирует операционная система и графические программы. А потом проверял их на соответствие к точкам принадлежащим идеальному кругу, с помощью теоремы Пифагора.
Идеальный круг 4-мя кривыми безье не сделать!
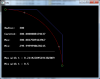
А теперь к практике. Я вчера добавил в программу пару функций, чтобы показывались самые проблемные места. (На рисунке два белых крестика). Можно их вычислить более точно. Координаты максимальной погрешности известны. В гипотетических единицах измерения это будет х=99,8642778032932, y=17,0226368238273. Находим арккосинус угла, переводим из радианов в градусы, получаем 19,4382189150887-гр.
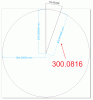
Открываем корел. Рисуем круг (можно побольше), например радиусом 300 мм. Рисуем линию от центра под углом 19.438. Мерим мерялкой.
Похож результат? Спрашивается, чего высчитывали академики?