Ответ: Как отрисовать фигуру "бесконечность" (повернутая 8), зная ее математическое уравнение?
Да что вы прицепились к Григорьеву с Малоземовым? Я не пойму, вы придуряетесь что ли - сказали же вам ясно - они совсем другую кривую описывают - пространственную, там даже рисунок есть для особо одаренных.
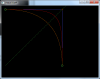
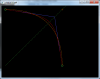
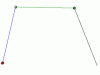
Тем не менее, вы гораздо умнее, чем пытаетесь показать, например, подход в посте 110 действительно гораздо более конструктивный, чем опираться на точку пересечения касательных. Я, к примеру, его взял исключительно из за простоты вычисления и оценки приближения. Гораздо более точное приближение дает аппроксимация квадратичным сплайном, который опирается на два конца дуги и серединную точку (как в случае с кубическим сплайном). Ни и это не самый оптимальный, оптимальный - примерно такой, как у вас на равом рисунке, но для его вычисления придется решать довольно сложную оптимизационную задачу. Да и надо ли? У нас ведь задача просто оценить погрешность не так ли? А по поводу "непохожести" - я ж вам и говорил, что так хорошо как кубическим не будет. Чем меньше степень тем хуже приближение, к примеру, отрезками (1 порядка) будет совсем хреново, зато 4 порядка - лучше чем кубическими.

 Еще раз повторюсь - приведенный PDF толкует о пространственных кривых Безье второго порядка, которые точно описывают окружность, действительно, тремя точками. У нас же в наличии обычные плоские, но третьего порядка. За неимением гербовой пишем на клозетной, как говорится.
Еще раз повторюсь - приведенный PDF толкует о пространственных кривых Безье второго порядка, которые точно описывают окружность, действительно, тремя точками. У нас же в наличии обычные плоские, но третьего порядка. За неимением гербовой пишем на клозетной, как говорится.